Reasearch of Connected Points in a 2-Dimensional Surface Area

This project's aim was to find the quickest way to identify the connected parts of points in a 2-dimensional surface area. A connected part of points is composed by 'close' points. Two points P1 and P2 are said to be 'close' if and only if the distance between them is inferior to s (with s defined). Given a list of points with their coordinates, the algorithm had to return a sorted list which contained the size of each connected part.

To identify the connected parts, we made distance tests between the points in the area. Thus, to optimise our algorithms during this project, our main focus was to minimise the relation between the number of tests which ended in d(p1, p2) ≤ s, and the whole number of tests.

First Method

Our first method was a brute one. For each point in the area, we almost tested the distance between it and all the other points. The algorithm works this way : - First, we store the points in a list. - Then we take the first point of this list and we add it to a list that we call connected-part. Then we remove the point from the points list et we call it center. - For the points left in the points list, if the distance between them and the center is inferior to s, then we add these points to the connected-part. The center becomes the next point in the connected part. If there is no next point, the connected part is complete and we store its size in a results list. - When there is no more point in the points list, the research is over.

VIEWING OF THE POINTS IN THE AREA

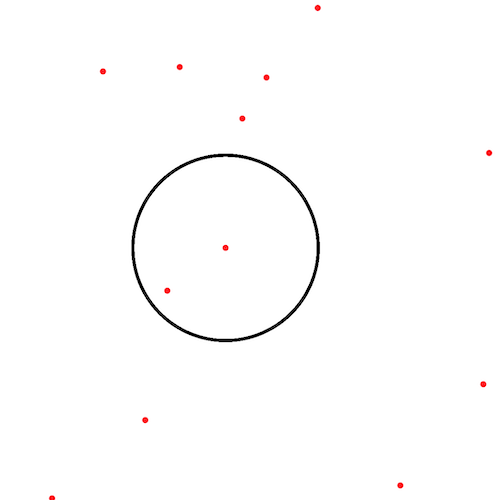
DISC WHERE THE DISTANCE BETWEEN THE CENTRE AND THE POINTS IS INFERIOR TO S

CONNECTED PARTS RETURNED

Optimising the algorithm

Our idea was to process the points beforehand. While we look over the list of points, the process will allow us to reduce the amount of distance tests. Here, we chose to join each point with a key describing its position in the surface area. Thus, we will only check the distance with points that are near the center. Here are the main ideas of the algorithm : - We store the points in a list - We begin with dividing the area into squares - We take the first point of the list, add it in a list we call connected-part, and remove it from the points list. - For every center in the connected-part, we check if the points that are in neighbouring cells are connected, if so we add them in the connected-part. - The center becomes the next point in the connected-part. If there is no next point, the connected part is complete and we store its size in a results list. - When there is no more point in the points list, the research is over.

PARTITION OF THE AREA

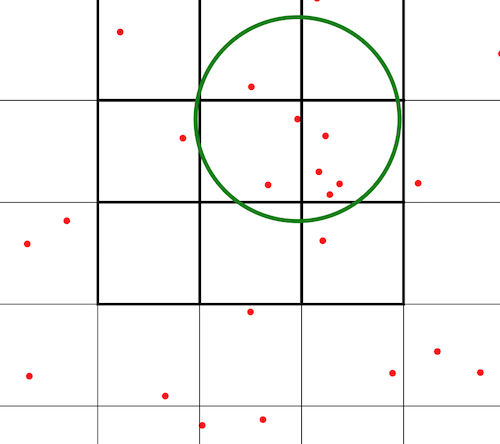
AN EXAMPLE OF RESEARCH : HERE, WE SEE THE NEIGHBOURING CELLS OF THE CENTER IN BOLD: THEIR POINTS WILL ALL BE TESTED. THE GREEN CIRCLE DELINEATES THE ZONE WHERE POINTS ARE FROM A GOOD DISTANCE TO THE CENTER.

To get further, we decided to divide the area in a quadtree. This lead to great results as well.

QUADTREE